Dissolving the Pentagram

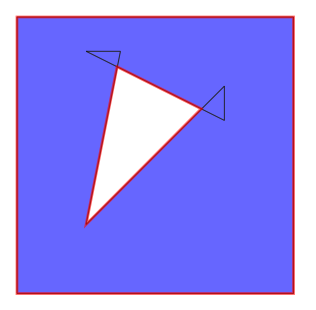
A week ago Denis asked the GGL-list if the internal segments of a self-intersecting polygon could be dropped. He attached this figure:


I answered that dissolve should do this. But it does not in this case. Dissolve can remove self-intersections, but under certain circumstances and even then it is not always perfect. So this is a reason to remove dissolve to the extensions folder - it should not yet be part of Boost.Geometry as it is released, hopefully in Boost 1.47

Pentagram

A pentagram is a five pointed star which can be drawn with a linestring of five segments. This is a Well-Known text presentation of a pentagram:

POLYGON((5 0,2.5 9,9.5 3.5,0.5 3.5,7.5 9,5 0))

As I often do, I compare the behaviour of algorithms on this WKT with SQL Server, PostGIS, and other packages (in this case Quantum GIS and SVG).

SVG

Boost.Geometry can create SVG images. This is really useful and I often use it in test programs. SVG's can then be depicted in FireFox. (In Google Chrome dropping the second SVG let it crash...).

SVG has thousands of properties, and one of them is the fill-rule. It can be set to winding and to non-zero. This delivers two different presentations:

winding	non-zero

SQL Server

In SQL Server the pentagram is drawn as such:


So it is using the winding rule.

The polygon is not valid, of course, it has five self-intersection points. SQL Server has a very good method to make polygons valid. It is obviously called MakeValid(). It is a SQL Server extension, not an OGC Method. I wrote "very good" and I mean that, we used it a lot in real-world problems and it has always worked very well.

With this specific pentagram MakeValid() creates a multi-polygon containing five triangles. So it directly uses the winding rule to create a multi-geometry. Sounds logical. If we calculate the area we get 17.7316840044235, the summed area of the five triangles. Calculating the area of a non-valid polygon is not possible in SQL Server. The statement is:

select geometry::STGeomFromText('POLYGON((5 0,2.5 9,9.5 3.5,0.5 3.5,7.5 9,5 0))',0)
.MakeValid().STArea()

PostGIS

PostGIS does not have a drawing engine. In PostGIS we can calculate the area of an invalid polygon and it gives us: 33.5. There is (AFAIK) not yet a function to make polygons valid, though it is announced. The good old trick is to use a buffer with buffer-distance 0, so we do this:

select ST_Area(ST_Buffer(ST_GeomFromText(
'POLYGON((5 0,2.5 9,9.5 3.5,0.5 3.5,7.5 9,5 0))',0),0))

and we get an area of 25.6158419936921. If we draw the zero-buffered result we get a filled polygon.

Boost.Geometry

Boost.Geometry can calculate the area of an invalid polygon and it also gives us: 33.5. The simple always-working Surveyor's formula just calculates this for us.

If we use the algorithm dissolve we indeed get a polygon with all internal corners dropped in this case. The area of the dissolved polygon is 25.6158412 and this is the right area. So the Surveyor's formula actually cannot be used with invalid polygons, SQL Server is right to prohibit this.

The SVG files displayed above are both created using Boost.Geometry so no picture here.

Quantum GIS

Quantum GIS has a great extension, QuickWKT, with which WKT geometries can be drawn. It uses the winding rule. It can calculate the area of the polygons (using the Info tool we can get it) and we get 33.5. Right, the Surveyor's formula.

What should happen

What should happen is not that simple. In these four programs, only SQL Server was consistent by prohibiting area calculation and creating a multi-geometry which looks like the image it depicts. All other programs and libraries were consistent, using the Surveyor's formula and creating a closed five-pointed polygon.

The reasoning of Boost.Geometry is that it takes direction into account. So if we draw arrows aside of all linestrings, we get:



And here we see, in the triangle with the smaller arrows, that the direction is not consistent. That triangle should not be generated. Of this whole pentagram several polygons can be drawn with consistent directions, and the largest of them is the whole polygon. So the dissolve function is expected to generate a five-pointed star here. And it does.

There is also a pentagon in the center with consistent directions. Because it has the same orientation as the outer polygon, it should be discarded. And it is. If it would have been orientated counterclockwise, a hole should have been formed.

So there are reasons to say that this pentagram indeed should be converted into a solid five-pointed star. There is no winding rule or non-zero rule involved there, it is just derived by the directions of the segments created by the intersection.

But now the sample

Anyway, using the sample of Denis Pesotsky, Boost.Geometry's results were not that clever. It generates two polygons which are indeed as expected, with consistent directions. The outer polygon does not have a consistent direction and therefore should not be generated, correct. But there is one polygon with consistent direction missing, in the lower right. That one is discarded but should not have been...



Because this, and because we have to think more about the behaviour, the dissolve algorithm has to be moved to the extensions folder. That means it will not be part of the initial release of Boost.Geometry, in the Release branch.

This is the WKT of the input polygon:

POLYGON((55 10, 141 237, 249 23, 21 171, 252 169, 24 89, 266 73, 55 10))

The white pieces are by the winding rule, and in SQL Server it is looking the same (no picture here). SQL Server's MakeValid() creates 9 polygons here.

PostGIS, using the buffer, creates one polygon, looking like this:


And that polygon is indeed the largest polygon which can be formed, following all arrows in clockwise direction. So this is the polygon that was expected by the dissolve algorithm...

Anyway, it is not the result that Denis asked for.

Useful usage

Dissolve can be very useful so I end this blog by just listing some of the testcases where it makes sense:

Inaccurate corners (extra intersection):



Messy corners:



Keyholed holes:

Conclusions

Due to shortcomings in the dissolve algorithm and vagueness in behaviour in general we have to move the dissolve function to the extensions folder. It has to be thought over more thoroughly.

Qt World Mapper with Boost.Geometry

Last year I created a simple world mapper using WxWidgets. For various reasons I decided to make the Qt equivalent as well.

Both Qt and WxWidgets are well-known cross-platform windows frameworks. Qt is used in Quantum GIS.

The World Mapper I created with WxWidgets did read world countries from a WKT (well-known text) file, and displayed them. Moving the mouse did highlight the country. For Qt it is similar (the highlighting is not yet been done).

The nice thing is that, by setting Boost.Geometry in this context, its force is shown:

Look below to lines marked with // Adapt. The QPointF and QPolygonF are just registered. From now on they act as normal Boost.Geometry geometries. So they can be used in area calculation, distance, transform, etc. We only use transform in this example.

So also look at lines commented with // This is the essention. Here a QPolygonF is declared, a ring (a normal Boost.Geometry part of a polygon, part of a multi-polygon) is transformed using the transformer to a QPolygonF. And the last one is of course displayed without any problem.

Delivering this application:

Complete C++ Code

#include <fstream> 

#include <QtGui> 
#include <QWidget> 
#include <QObject> 
#include <QPainter> 

#include <boost/foreach.hpp> 

#include <boost/geometry/geometry.hpp> 
#include <boost/geometry/geometries/register/point.hpp>
#include <boost/geometry/geometries/register/ring.hpp>

#include <boost/geometry/multi/multi.hpp> 
#include <boost/geometry/extensions/algorithms/selected.hpp>
#include <boost/geometry/extensions/gis/io/wkt/wkt.hpp> 

// Adapt a QPointF such that it can be handled by Boost.Geometry
BOOST_GEOMETRY_REGISTER_POINT_2D_GET_SET(QPointF, double, cs::cartesian, x, y, setX, setY)

// Adapt a QPolygonF as well. 
// A QPolygonF has no holes (interiors) so it is similar to a Boost.Geometry ring
BOOST_GEOMETRY_REGISTER_RING(QPolygonF) 

typedef boost::geometry::model::d2::point_xy<double> point_2d; 
typedef boost::geometry::model::multi_polygon 
    < 
        boost::geometry::model::polygon<point_2d> 
    > country_type; 


class WorldMapper : public QWidget
{ 
public: 
    WorldMapper(std::vector<country_type> const& countries, boost::geometry::model::box<point_2d> const& box)
        : m_countries(countries) 
        , m_box(box) 
    { 
        setPalette(QPalette(QColor(200, 250, 250)));
        setAutoFillBackground(true); 
    } 

protected: 
    void paintEvent(QPaintEvent*) 
    { 
        map_transformer_type transformer(m_box, this->width(), this->height()); 

        QPainter painter(this); 
        painter.setBrush(Qt::green); 

        BOOST_FOREACH(country_type const& country, m_countries)
        { 
          typedef boost::range_value<country_type>::type polygon_type;
          BOOST_FOREACH(polygon_type const& polygon, country)
          { 
           typedef boost::geometry::ring_type<polygon_type>::type ring_type;
           ring_type const& ring = boost::geometry::exterior_ring(polygon);

           // This is the essention: 
           // Directly transform from a multi_polygon (ring-type) to a QPolygonF 
           QPolygonF qring; 
           boost::geometry::transform(ring, qring, transformer); 

           painter.drawPolygon(qring); 
          } 
       } 
    } 

private: 
    typedef boost::geometry::strategy::transform::map_transformer
        < 
          point_2d, QPointF, 
          true, true 
        > map_transformer_type; 

     std::vector<country_type> const& m_countries;
     boost::geometry::model::box<point_2d> const& m_box;
}; 


class MapperWidget : public QWidget
{ 
public: 
     MapperWidget(std::vector<country_type> const& countries, boost::geometry::model::box<point_2d> const& box, QWidget *parent = 0)
         : QWidget(parent) 
     { 
         WorldMapper* mapper = new WorldMapper(countries, box);

         QPushButton *quit = new QPushButton(tr("Quit")); 
         quit->setFont(QFont("Times", 18, QFont::Bold)); 
         connect(quit, SIGNAL(clicked()), qApp, SLOT(quit())); 

         QVBoxLayout *layout = new QVBoxLayout; 
         layout->addWidget(mapper); 
         layout->addWidget(quit); 
         setLayout(layout); 
     } 

}; 


template <typename Geometry, typename Box>
inline void read_wkt(std::string const& filename, std::vector<Geometry>& geometries, Box& box)
{ 
    std::ifstream cpp_file(filename.c_str()); 
    if (cpp_file.is_open()) 
    { 
        while (! cpp_file.eof() ) 
        { 
          std::string line; 
          std::getline(cpp_file, line); 
          if (! line.empty()) 
          { 
              Geometry geometry; 
              boost::geometry::read_wkt(line, geometry); 
              geometries.push_back(geometry); 
              boost::geometry::combine(box, boost::geometry::make_envelope<Box>(geometry)); 
          } 
        } 
    } 
} 

int main(int argc, char *argv[])
{ 
    std::vector<country_type> countries; 
    boost::geometry::model::box<point_2d> box; 
    boost::geometry::assign_inverse(box); 
    read_wkt("../data/world.wkt", countries, box); 

    QApplication app(argc, argv); 
    MapperWidget widget(countries, box); 
    widget.setWindowTitle("Boost.Geometry for Qt - Hello World!"); 
    widget.setGeometry(50, 50, 800, 500);
    widget.show(); 
    return app.exec(); 
}

Conclusions

With less than 160 lines of code, Qt and Boost.Geometry we showed how it can quite conveniently combine together.
The source is shown above and in SVN it can be found here.

Actually this application (and its WxWidgets counterpart) was for me the reason to start the shapefile research, which final conclusions still have to be drawn.

Spikes: research with ESRI

A short follow-up on my previous blog about spikes and their causes. My collegue Bert recoded the scenario in C# using ESRI. Thanks Bert! The full code is shown below.

The answer is this: with ESRI the spikes are not there. The program produces:

area: 295.44447138901, perimeter: 92.5058167188044

select geometry::STGeomFromText ('POLYGON((180956.436999999
313716.998,180953.978700001 313701.0152,180926.420299999
313732.510699999,180954.359000001
313720.504000001,180956.436999999 313716.998,180956.436999999
313716.998))', 28992)

And this result is right, area and perimeter are without spikes and if you visualize this WKT (e.g. with SQL Server) you get the right picture...

Interesting is that all coordinates seems to be rounded on one millimeter or a tenth of it. That is probably the result of the fuzzy tolerance policy that ESRI uses. Personally I'm normally a bit sceptic about that approach: though it can avoid spikes and slivers, it also brings some fuzzyness into the result. It is sometimes quite hard to determine a tolerance which is sufficient for cleaning and sufficient for not destroying features... Anyway, in this scenario it works well.

It seems interesting to check, if you use rounding in e.g. Boost.Geometry, would the spikes be gone... The answer is (of course), sometimes yes, sometimes no. The rounding is applied on a larger grid, so the effect remains the same. Rounding is not enough. To get rid of spikes, in this scenario, the spike removal functionality is advised. Which uses a gap distance, which can be seen as a sort of fuzzy tolerance...

C# Code for "difference after cut" with ESRI

using System; 
using System.Collections.Generic; 
using System.ComponentModel; 
using System.Data; 
using System.Drawing; 
using System.Text; 
using System.Windows.Forms; 
using ESRI.ArcGIS.Geometry; 
using ESRI.ArcGIS.esriSystem; 
using Microsoft.SqlServer.Types; 
using System.Data.SqlTypes; 

namespace SpikesResearchWithEsri 
{ 
    public partial class Form1 : Form
    { 
        public Form1() 
        { 
          InitializeComponent(); 
        } 

        private void InitializeLicense()
        { 
          AoInitialize aoi = new AoInitializeClass(); 

          //Additional license choices can be included here. 
          esriLicenseProductCode productCode = 
          esriLicenseProductCode.esriLicenseProductCodeArcEditor; 
          if (aoi.IsProductCodeAvailable(productCode) == 
          esriLicenseStatus.esriLicenseAvailable) 
          { 
          aoi.Initialize(productCode); 
          } 
        } 


        private void button1_Click(object sender, EventArgs e)
        { 


          ESRI.ArcGIS.RuntimeManager.Bind(ESRI.ArcGIS.ProductCode.Desktop); 
          InitializeLicense(); 
          IPolygon parcel = this.GetParcel(); 
          IPolyline line = this.GetCutLine(); 

          IPolygon bufferedLine=(IPolygon)((ITopologicalOperator)line).Buffer(0.1); 
          
          IGeometry result=((ITopologicalOperator)parcel).Difference(bufferedLine); 
          IPolygon4 p = (IPolygon4)result; 

          // Big part: 
          IPolygon firstPolygon = this.GetPolygon(p, true);
          // Small part: 
          IPolygon secondPolygon = this.GetPolygon(p, false);


          // use if we do a cutpolygon 
          //IGeometry leftPolygon; 
          //IGeometry rightPolygon; 
          //((ITopologicalOperator)parcel).Cut(line, out leftPolygon, out rightPolygon); 
          //IPolyline cutline=(IPolyline)((ITopologicalOperator)(ICurve)parcel).Intersect(line, esriGeometryDimension.esriGeometryNoDimension); 
          //IPolygon firstPolygon = (IPolygon)leftPolygon; 
          //IPolygon secondPolygon = (IPolygon)rightPolygon; 
          //this.textBox1.Text=("from: " + cutline.FromPoint.X.ToString() + ", " + 
          // cutline.FromPoint.Y.ToString() + ", " + 
          // "to: " + cutline.ToPoint.X.ToString() + ", " + 
          // cutline.ToPoint.Y.ToString()) + Environment.NewLine; 

          this.textBox1.Text += "Small polygon stats: " + System.Environment.NewLine; 
          this.textBox1.Text += GetStats(secondPolygon); 
          this.textBox1.Text += GetWkt(secondPolygon); 

          // now calculate the difference between original and the big part (result should be the small part) 
          IPolygon4 pol2= (IPolygon4)((ITopologicalOperator)parcel).Difference(firstPolygon); 
          this.textBox1.Text += "Result Small polygon stats: " + System.Environment.NewLine; 
          this.textBox1.Text += GetStats(pol2); 
          this.textBox1.Text += GetWkt(pol2); 
        } 

        private string GetStats(IPolygon pol)
        { 
          double area = ((IArea)pol).Area; 
          double perimeter = ((ICurve)pol).Length; 
          return "area: " + area.ToString() + ", perimeter: " + perimeter.ToString() + System.Environment.NewLine; 
        } 


        private string GetWkt(IPolygon pol)
        { 
          string res = GeomHelper.aoGeomToWkt(pol, false, 28992);
          res = res.Substring(0, res.Length - 1);
          string print = "select geometry::STGeomFromText ('" + res + "', 28992)" + Environment.NewLine; 
          return print; 
        } 

        public IPolygon GetPolygon(IPolygon4 input, bool first)
        { 
          IGeometryBag exteriorRings = input.ExteriorRingBag; 
          IEnumGeometry exteriorRingsEnum = exteriorRings as IEnumGeometry;
          exteriorRingsEnum.Reset(); 

          IRing firstRing = exteriorRingsEnum.Next() as IRing;
          IPointCollection pcFirst = (IPointCollection)firstRing; 

          IRing secondRing = exteriorRingsEnum.Next() as IRing;
          IPointCollection pcSecond = (IPointCollection)secondRing; 

          IPolygon p = new PolygonClass(); 

          if(first)((IPointCollection)p).AddPointCollection(pcFirst); 
          if(!first)((IPointCollection)p).AddPointCollection(pcSecond); 
          return p; 
        } 


        private IPolygon GetParcel() 
        { 
          string wkt = "POLYGON ((180956.437 313716.998, 180954.359 313720.504, 180906.303 313741.156, 180896.82 313744.272, 180890.456 313748.17, 180831.49 313797.135, 180809.668 313816.098, 180776.418 313842.336, 180771.483 313846.102, 180746.934 313843.764, 180731.738 313840.386, 180717.32 313833.763, 180710.827 313828.438, 180704.982 313820.515, 180699.267 313811.813, 180698.488 313801.162, 180700.826 313793.889, 180705.539 313791.06, 180706.021 313790.771, 180710.156 313789.208, 180766.157 313768.042, 180825.515 313744.013, 180878.636 313724.271, 180945.593 313695.884, 180952.801 313693.358, 180956.437 313716.998))"; 
          IGeometryFactory factory = new GeometryEnvironmentClass();
          SqlGeometry g = SqlGeometry.Parse(wkt); 
          IGeometry geom2 = new PolygonClass(); 
          int countout; 
          factory.CreateGeometryFromWkbVariant(g.STAsBinary().Value, out geom2, out countout);
          geom2.SpatialReference = this.GetProjectedSpatialReference(28992);
          return (IPolygon) geom2; 
        } 

        private IPolyline GetCutLine() 
        { 
          string line = "LINESTRING(180955 313700,180920 313740)"; 
          IGeometryFactory factory = new GeometryEnvironmentClass();
          SqlGeometry g = SqlGeometry.Parse(line); 
          IGeometry geom2 = new PolylineClass(); 
          geom2.SpatialReference = this.GetProjectedSpatialReference(28992);
          int countout; 
          
          factory.CreateGeometryFromWkbVariant(g.STAsBinary().Value, out geom2, out countout);
          return (IPolyline)geom2; 

        } 


        private ISpatialReference GetProjectedSpatialReference(int pcsType)
        { 
          ISpatialReferenceFactory pSRF = new SpatialReferenceEnvironmentClass();
          IProjectedCoordinateSystem m_ProjectedCoordinateSystem = pSRF.CreateProjectedCoordinateSystem(pcsType);
          ISpatialReference spatialReference = (ISpatialReference)m_ProjectedCoordinateSystem; 
          return spatialReference; 
        } 

    } 
}