Precision, the cause of spikes

This is a follow-up on my last blog. The spikey effects we have seen are perfectly explainable and understandable.

What we did was:

1. cut a parcel in two pieces
1. create a cutline and make a (nearly linear) cutting polygon of it (using buffer)
2. subtract that cutline from the geometry, using STDifference
2. keep one piece, using STGeometryN
3. subtract that piece from the parcel, using STDifference

The result should be the discarded piece, but we got back two free spikes extra.

This short blog will explain this a little more and, as a side note, use just another SQL syntax for the same result.

Side note: with

The query from my previous blog can be rewritten much more elegantly using the with syntax:

with myquery as 
(
  select
    geometry::STGeomFromWKB(0x0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341,28992)
      as parcel,
    geometry::STGeomFromText('LINESTRING(180955 313700,180920 313740)', 28992).STBuffer(0.1)
      as cutline
)
select parcel.STDifference((select parcel.STDifference(cutline).STGeometryN(2) from myquery))
from myquery

The with clause is useful to avoid repeating pieces (as having the WKB twice), and is essential to do recursive queries. You define an inlined viewy thingy (here "myquery") and use it.

Both SQL Server and PostGreSQL support with queries. See also this link which explains with in depth.

Floating point precision

Floating points are really awful. Everyone knows that if you divide one by six (1/6) and multiply the result with six ((1/6) * 6) you should get one back. However, with floating points this is not always the case. You might get 0.9999999 back. If you try it, you might also get the correct 1.0 back. That is (according to this book) because intermediate results are stored in the floating point register of the CPU. So it is by chance that it is right. In reality it will be wrong.

See also this link and scroll to "Rounding errors can play havoc with math-intense programs". Adding ten 0.1 values will result into 0.99999999999999989. I repeated this and indeed this is the case with a double. With a float the result is 1.0000001192092896. With ttmath it is 1.0, but as soon as you do the same trick with eleven 1/11 additions, you might get 0.9999999999999999999999999999999 back, or 1.0, depending on which precision you specify. Using Boost.Rational you get always 1/1, guaranteed, because it calculates in another way. It uses fractions and keeps fractions all the time. That is great in this use case.

What then caused the spikes

Now that we realize again that floating points are awful, we investigate how imprecision causes the spikes. The damage happens in the first phase. The first STDifference is used to cut the parcel into two pieces.

See the picture below. The grid is the so-called floating point grid. The smallest difference in a 32 bits floating point value (1.175e-38) is depicted. Any point (with float) must be located on one of the gridpoints. (In reality the FP-grid is irregular, but the idea will be clear).

So in this case (in most cases), the intersection point happens to fall between the gridpoints... All the vertices of both input polygons are located on the gridpoints, of course. But the real intersection point does not. It is rounded to one of the four gridpoints. It is just by chance to which one it is rounded. So the rounded intersection point is located on a gridpoint.




Suppose it rounds to the point labeled "3". We then get a resulting polygon as partly depicted here:




The resulting polygon (in blue) is too small. There is a small piece of the original polygon which is not covered by this piece, at the north side, upperleft of point 3. Subtract this resulting polygon from the original and of course, you will get the spike. There is also a similar small piece at the east side but that will not create a visual effect in this use case.

There is no obvious solution. It is the same as adding ten times 0.1. You get too much or too little. These spikes are too little in the first phase, and after the second difference, the two resulting spikes are a bit too much. This explains that sometimes you get zero, sometimes you get one and sometimes you get two spikes. It is by chance. If the rounding would go to point "1" in the picture above, there would be no spike there.

The spikes are not the result of flawed logic, or wrong decisions somewhere. It is just the rounding.

Use ttmath if you want to minimize the chance on it. Or work around it, e.g. by buffering the result with a small value e.g. -0.000001. Boost.Geometry now has some algorithms to find spikes and remove them.

By the way, the nice trick on cutting a parcel into two pieces was introduced in our project by our partners from B3Partners. The project where this study is from extracted is the Portaal Natuur en Landschap

Conclusions

In this use case, spikes are the geometric visualization of floating point imprecision.

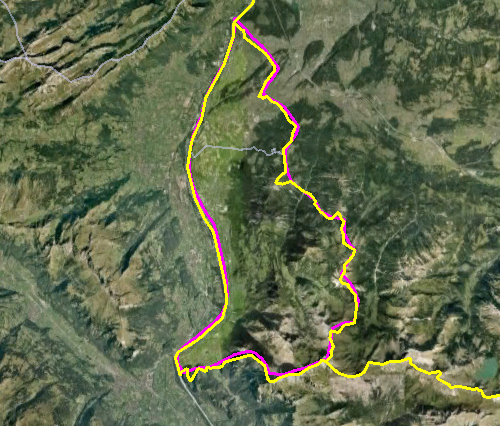
SQL Server, PostGIS, STDifference and Precision

Today I encountered a problem related to the OGC difference function. I will describe this problem in this blog. I created a sort of minimal sample, without database, and present that here.

The problem

The problem I encountered is precision: both SQL Server (where I encountered it) and PostGIS (where I verified it) do not handle the situation described here sufficiently. The results is a polygon with two spikes which should not be there. The cause must be imprecision of floating point types. The message is: be warned!

The situation is as following: there is a parcel. That parcel is cut into two pieces (I will explain below how). One piece is thrown away, the other piece is kept. That kept piece is subtracted from the original parcel. What you would expect is having the original piece that was earlier thrown away. But what is happening is that you get one or two spikes extra...

The parcel and the cutline are shown here:

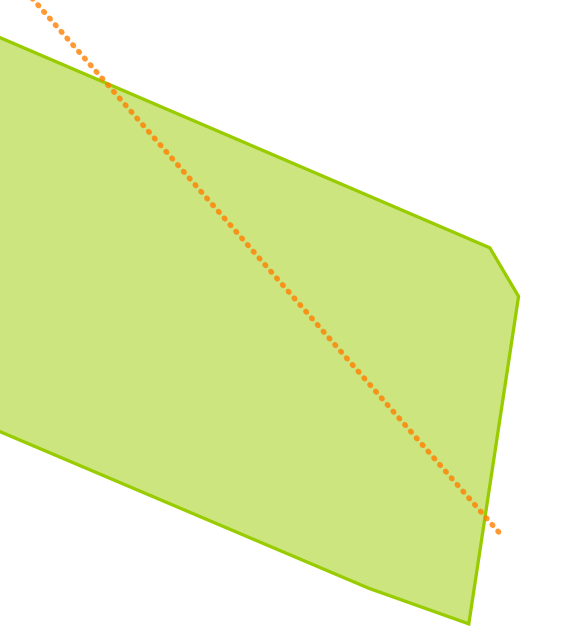
Cutting into two pieces

We cut (for this experiment) the polygon into two pieces by buffering the cutline, and subtracting (with STDifference) that from the parcel. The cutline is shown in the figure above as the dotted red line. Then we keep one of the two resulting polygons using the STGeometryN function. By trying we get the left piece which we want to keep by index 2.

So this piece of SQL is, for SQL Server:

select geometry::STGeomFromWKB(0x0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341,28992)
.STDifference(geometry::STGeomFromText('LINESTRING(180955 313700,180920 313740)', 28992).STBuffer(0.1)).STGeometryN(2)

And for PostGIS it is:

select ST_GeometryN(ST_Difference(
ST_SetSRID('0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341'
 ::geometry, 28992)
, (ST_Buffer(ST_GeomFromText('LINESTRING(180955 313700,180920 313740)',28992),0.1))), 2)

Note that the 28992 is just an SRID of a coordinate system (the Dutch), it probably works (or better stated: does not work) with any coordinate system. The result is this:

Subtracting one of the pieces from the original

After cutting we subtract the piece we kept from the original parcel. This will result in the other piece. In fact we get the area covered by the small buffer as well, but that is hardly visible, and is not important for this story.

This is how it should look like:



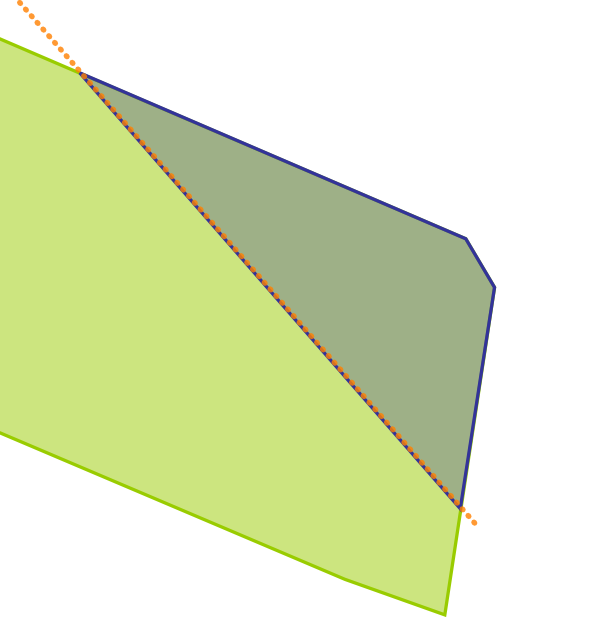
And this is the complete query in SQL Server:

select
geometry::STGeomFromWKB(0x0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341,28992)
.STDifference
(
  (
 select 
 geometry::STGeomFromWKB(0x0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341,28992)
 .STDifference(geometry::STGeomFromText('LINESTRING(180955 313700,180920 313740)', 28992).STBuffer(0.1)).STGeometryN(2)
 )
)

And in PostGIS:

select ST_Perimeter(ST_Difference(
ST_SetSRID('0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341'::geometry,28992)
,
(select ST_GeometryN(ST_Difference(
ST_SetSRID('0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341'::geometry,28992)
,(ST_Buffer(ST_GeomFromText('LINESTRING(180955 313700,180920 313740)', 28992),0.1))),2)
)))

Results

To my surprise I got two spikes in SQL Server. To verify this, I looked into PostGIS. I got two spikes as well. First I thought it was caused by precision, going to WKT and back. But also if you use WKB, or if you use the geometry from the underlying database (not shown here), you will get the same. So it is the imprecision of the handling. When varying the cutline a bit (changing 180955 to 180960), I get one spike in SQL Server and still two in PostGIS.

The spikes are shown here, bordering the blue result:


The perimeter of the result is interesting. The result, without spikes, should be 92.5 meter. But including the spikes it is 151.792871568541 (in SQL Server, using the function .STLength() and 151.792880859545 (in PostGIS, using the function ST_Perimeter(...).

The area is everywhere about 295.4 square meter, with or without spikes, indicating that the spikes have an area about zero (so those are real spikes).


Why would you do such a thing... Creating a parcel, cutting, throwing away one, subtracting and getting the other one...

Well, I was just testing our application. Our application has WebGIS functionality to create parcels. And to cut parcels into two pieces. And to throw away pieces. And to fill-up space which is left from a parcel and a piece. So just this scenario. And to my annoyance, often you get spikes! This project is done with SQL Server, and we get spikes. But this little research shows that, would we have done it with PostGIS, we would have had resulting spikes as well.

It is as a simple mathematical exercise. We cut 5 into two pieces, 3 and 2. We throw away the 2 and keep the 3. We subtract 3 from our 5. And we get the 2 back, of course. In geometry we subtract (difference) twice but that is just because the cut is not an OGC operation. So we trick it.

Note that I didn't get this just once. I got it several times for different geometries. Note also that it can easily be solved using a STBuffer of -0.00001 on the resulting polygon, which will eliminate the spikes and have no visual impact (it has an impact though...).

With Boost.Geometry

Of course I was curious what Boost.Geometry would do with this.

The buffer of Boost.Geometry is not completely implemented, so I create the buffer in SQL Server, saving the WKB.

select geometry::STGeomFromText('LINESTRING(180955 313700,180920 313740)', 28992).STBuffer(0.1).STAsBinary()

and draft some C++ code:

template <typename T> 
void test_difference_parcel_precision() 
{
    namespace bg = boost::geometry; 
    typedef bg::model::d2::point_xy<T> point_type; 
    typedef bg::model::polygon<point_type> polygon_type;
    typedef std::vector<boost::uint8_t> byte_vector;

    polygon_type parcel, buffer; 

    { 
        byte_vector wkb; 
        bg::hex2wkb("0103000000010000001A00000023DBF97EE316064146B6F3FDD32513415A643BDFD216064175931804E225134196438B6C52150641C976BE9F34261341F6285C8F06150641022B871641261341F853E3A5D3140641E17A14AE50261341B81E85EBFB120641A4703D8A142713414E6210584D120641AC1C5A64602713414E621058431106414E621058C9271341A01A2FDD1B11064121B07268D8271341F4FDD478571006411904560ECF271341448B6CE7DD0F06418195438BC1271341F6285C8F6A0F06413BDF4F0DA72713410E2DB29D360F06416F1283C091271341E5D022DB070F0641F6285C0F7227134160E5D022DA0E06416F1283404F271341448B6CE7D30E0641F853E3A52427134154E3A59BE60E06411904568E07271341643BDF4F0C0F0641D7A3703DFC2613414A0C022B100F064125068115FB26134191ED7C3F310F0641B6F3FDD4F42613414C378941F11006414A0C022BA0261341EC51B81ECC1206413BDF4F0D40261341022B87167514064125068115F1251341B4C876BE8C160641C74B37897F25134121B07268C6160641508D976E7525134123DBF97EE316064146B6F3FDD3251341", std::back_inserter(wkb)); 
        bg::read_wkb(wkb.begin(), wkb.end(), parcel); 
    } 
    { 
        byte_vector wkb; 
        bg::hex2wkb(
"01030000000100000083000000000032FCD716064100009E998F25134100000706D81606410040A4998F2513410000DA0FD816064100C0E6998F2513410000A819D81606410080659A8F25134100806A23D816064100C0209B8F25134100801E2DD81606410080189C8F2513410000BE36D816064100404D9D8F25134100004540D816064100C0BE9E8F2513410000AF49D816064100806DA08F2513410000F752D8160641008059A28F2513410000195CD816064100C082A48F25134100800F65D81606410080E9A68F2513410000D66DD816064100408EA98F25134100006876D816064100C070AC8F2513410000C17ED8160641000091AF8F2513410080DC86D816064100C0EFB28F25134100009E8ED816064100C081B68F2513410080EC95D816064100803ABA8F2513410080C79CD8160641000018BE8F25134100002FA3D8160641008017C28F251341008022A9D8160641000037C68F2513410080A1AED8160641000074CA8F2513410000ACB3D81606410040CCCE8F251341000042B8D816064100403DD38F251341000062BCD81606410000C5D78F25134100000DC0D8160641000061DC8F251341000042C3D816064100000FE18F251341000001C6D81606410080CCE58F251341008049C8D8160641004097EA8F25134100001BCAD816064100006DEF8F251341008075CBD816064100804BF48F251341008058CCD8160641004030F98F2513410000C4CCD8160641000019FE8F2513410080B7CCD81606410080030390251341008032CCD81606410000ED0790251341000035CBD81606410000D40C902513410080BEC9D81606410040B511902513410000CFC7D816064100408F1690251341008065C5D816064100005F1B90251341008082C2D81606410080222090251341000025BFD81606410080D7249025134100004DBBD816064100807B29902513410080FAB6D816064100800C2E9025134100002DB2D816064100C08732902513410080E3ACD81606410000EB369025134100801EA7D81606410000343B902513410000DEA0D81606410080603F902513410080209AD816064100406E43902513410080209AC015064100406E43302613410080FC92C015064100004F473026134100008B8BC01506410040F64A302613410000D083C015064100C0634E302613410000D17BC0150641008097513026134100009273C015064100409154302613410000186BC015064100C050573026134100806762C01506410000D6593026134100808559C01506410000215C3026134100007650C01506410000315E3026134100003E47C015064100800660302613410000E23DC01506410000A1613026134100006734C015064100800063302613410080D12AC015064100C024643026134100002621C015064100800D653026134100006917C015064100C0BA653026134100809F0DC015064100402C66302613410000CE03C015064100006266302613410000F9F9BF15064100C05B6630261341000026F0BF1506410040196630261341000058E6BF15064100809A6530261341008095DCBF1506410040DF64302613410080E1D2BF1506410080E76330261341000042C9BF15064100C0B262302613410000BBBFBF1506410040416130261341000051B6BF1506410080925F30261341000009ADBF1506410080A65D302613410000E7A3BF15064100407D5B302613410080F09ABF150641008016593026134100002A92BF15064100C071563026134100009889BF15064100408F533026134100003F81BF15064100006F503026134100802379BF1506410040104D3026134100006271BF15064100407E49302613410080136ABF1506410080C5453026134100803863BF1506410000E841302613410000D15CBF1506410080E83D302613410080DD56BF1506410000C9393026134100805E51BF15064100008C35302613410000544CBF15064100C03331302613410000BE47BF15064100C0C22C3026134100009E43BF15064100003B28302613410000F33FBF15064100009F23302613410000BE3CBF1506410000F11E302613410000FF39BF1506410080331A302613410080B637BF15064100C06815302613410000E535BF150641000093103026134100808A34BF1506410080B40B302613410080A733BF15064100C0CF063026134100003C33BF1506410000E7013026134100804833BF1506410080FCFC2F2613410080CD33BF150641000013F82F2613410000CB34BF15064100002CF32F26134100804136BF15064100C04AEE2F26134100003138BF15064100C070E92F26134100809A3ABF1506410000A1E42F26134100807D3DBF1506410080DDDF2F2613410000DB40BF150641008028DB2F2613410000B344BF150641008084D62F26134100800549BF1506410080F3D12F2613410000D34DBF150641004078CD2F26134100801C53BF150641000015C92F2613410080E158BF1506410000CCC42F2613410000225FBF15064100809FC02F2613410080DF65BF15064100C091BC2F2613410080DF65D716064100C091BC8F2513410080036DD71606410000B1B88F25134100007574D716064100C009B58F2513410000307CD716064100409CB18F25134100002F84D7160641008068AE8F25134100006E8CD716064100C06EAB8F2513410000E894D71606410040AFA88F2513410080989DD716064100002AA68F25134100807AA6D71606410000DFA38F25134100008AAFD71606410000CFA18F2513410000C2B8D71606410080F99F8F25134100001EC2D716064100005F9E8F251341000099CBD71606410080FF9C8F25134100802ED5D71606410040DB9B8F2513410000DADED71606410080F29A8F251341000097E8D71606410040459A8F251341008060F2D716064100C0D3998F251341000032FCD716064100009E998F251341", std::back_inserter(wkb)); 
        bg::read_wkb(wkb.begin(), wkb.end(), buffer); 
    } 
    bg::correct(parcel); 
    bg::correct(buffer); 

    std::vector<polygon_type> pieces; 
    bg::difference(parcel, buffer, pieces); 

    std::vector<polygon_type> filled_out; 
    bg::difference(parcel, pieces.back(), filled_out); 

    std::cout << std::setprecision(16) << bg::wkt(filled_out.front()) << std::endl; 
    std::cout << bg::area(filled_out.front()) << std::endl; 
    std::cout << bg::perimeter(filled_out.front()) << std::endl; 
}

We are using WKB here to not loose precision. I run this with three different numeric types (float, double and ttmath high precision). And that is the essence of Boost.Geometry! Not one type! Many types! All types!

int main(int, char* [])
{ 
    test_difference_parcel_precision<float>(); 
    test_difference_parcel_precision<double>(); 
    test_difference_parcel_precision<ttmath_big>(); 
    return 0; 
}

Using these three types we get:

• float: one spike, perimeter 136.28
  
• double: two spikes, perimeter 151.793
  
• ttmath: zero spikes, correct result, perimeter 92.50548050416428971188559805054187252

Conclusions

• SQL Server is not perfect, it can cause spikey features
  
• PostGIS is not perfect, it can cause spikey features
  
• The cause is not WKT, nor it is WKB
  
• Boost.Geometry, using double, is not perfect because it causes the same spikey features
  
• Boost.Geometry, using ttmath, gives the correct results
  
• Boost.Geometry, using float, gives one spikey feature
  
• Changing the cutline a bit causes only one spikey feature within SQL Server, still two in PostGIS, and zero in Boost.Geometry (with all numeric types).
  
• Be aware of floating point precision

Free Shapefiles of Countries of the World (4)

There was the suggestion to look at gadm (Global Administrative Areas), thanks for this suggestion. This blog handles this new source in detail. Note that some sources are apparently hard to find, i.e. not found immediately by googling to "world country shapefiles" or similar. I'm glad that this blog appears now in the first 10 results, so hope to provide by this an index to world country shapefiles.

Look also at  part 1,  part 2, and part 3 of this blog.

Large

This newly found shapefile is very interesting. The first observation is that it is rather large, the zipfile is 158MB and takes several minutes of downloading. Unzipped the triplet (shp,shx,dbf) is almost half a gigabyte. When we zoom in, we see how this is caused, it is a shapefile taken from a grid:




The image above is a piece of the island Elba, the magenta line is the kml-ified shapefile displayed in Google Earth (yes, I like Google Earth).

I don't know if I like all those cornery borders... At least, it is not necessary to keep them, why are they not dropped or generalized away?

Anyway, if we zoom out a little again, the borders seem to be reasonably accurate at the first sight, here is the whole island Elba:

Vatican City and Liechtenstein

In last blog I described the small countries in and around Italy. So I shortly redo this for this new datasource. The gadm contains really the most accurate approximatino of Vatican City, compared with Google Earth as still our Single Point of Truth...



It is much better than all other sources found, and it therefore raises an interesting question: what is that little block where it differs, just to the southwest of Saint Peter's Square? Who is right there? And who is wrong? Interesting questions in the neighbourhood of the heart of the Roman Church... But we mean it geographically. Is Google failing here, as in Nicaragua and Costa Rica, nearly causing a war? Or is it the gadm.org website, a particular initiative providing freely available shapefiles for academic and non-commercial use (e.g. blogging)? According to Wikipedia, there indeed is a border dispute near Vatican City, but that is a little more to the east...

And look, we see a similar issue with Liechtenstein, probably a disputed valley...



But for the rest also here this shapefile is relatively accurate. For its size, accuracty is expected, of course...

Monaco

In last blog we saw that the borders of Monaco were correct in only one of the compared shapefiles... Alas, wrong again here:



It seems hard to create a correct shapefile... What is the source of all those errors? Who is really right here? Of course Google! For all certainty I checked this at Wikipedia (because I've never been in Monaco). Yes, the yellow line of Google is following Monaco's portrayal within the Wiki page of Monaco. So alas, gadm is totally wrong here.

The Netherlands

I'm living there, in that little country which is so difficult to be stored in free shapefiles... There is really a large lake, only bordered from the sea by a dike. That lake should be displayed, and it is not. If very small and uninhabited islands are displayed, the lake should really be there. And it is not the only error, in Zeeland the (smaller) water bodies behind the dikes are omitted as well.

The Caspian Sea

This was another requirement (CS1). It is not as bad as it was in some other shapefiles, where the Caspian Sea was divided between surrounding countries. But the Caspian Sea is included as a separate country in gadm... Interesting. Do they issue passports?

Validity

Finally there is validity. All countries should be modelled as multi-polygons and be valid in both SQL Server and PostGIS. We've already seen that this requirement is met in only one caes, until now (11). And also for this case, 13, alas, there are many multi-polygons invalid in SQL Server. In PostGIS it is OK, though the query runs for a long time due to the excessive size of  the geometries. The values are post-editted in the previous blog.

Actually it is nice to show a variant of the query, using the with syntax:

with valid as (select ST_IsValid(the_geom) as v from world13)
select v,count(1) from valid group by v;

Conclusion

As always I'm glad with new shapefiles. This one is quite accurate, and in many aspects the best until now. But also, it is way too large, too cornery, and contains errors, as all others do...

So I think a good and freely available shapefile of the countries of the world is still very welcome.

If there are more shapefiles, I'm still interested, but especially I'm interested in a the Google country borders in any format? Are they available?