Intersections (2), "recursive polygons"

The Boost.Geometry review report said:

Testing: several reviewers mentioned the need for a thorough testing framework allowing the verification of the correctness of the algorithms in a wide range of use cases. Different test strategies need to be employed, such as high volume and random tests, known border case tests, tests using different numeric precision types, etc.

This blog will discuss a part of this, a program called recursive_polygon.cpp, which is a test in the category high volume an random, using different numeric precision types.

Recursively made polygons

In this testprogram, polygons are created in a recursive way. In the first step two polygons are created. They are created at a random place and either a box, or a triangle (in this case: a box with one coordinate omitted). The first version of the program was called recursive_boxes because it then did only boxes. Those two polygons are unioned and the result is either a polygon, or a multi-polygon. In the first step, it is probably a multi-polygon.

After this, two other polygons like this, based on random coordinates, are unioned and result in another multi-polygon.

In the second step, the results of these two earlier unioned multi-polygons are again unioned. This will deliver a third multi-polygon. And so the process goes on, each time creating more complex multi-polygons, and after a a while holes are generated, self-tangencies.

The figure below shows the idea more clearly.



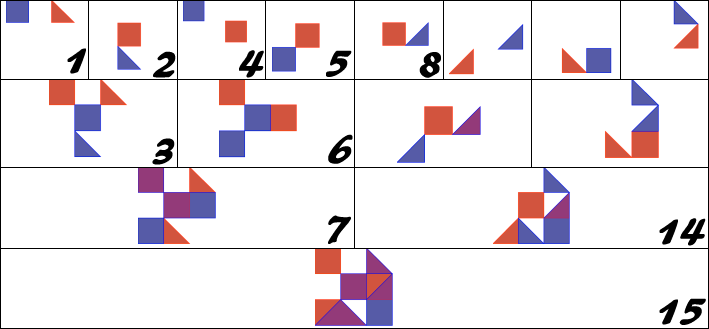
In this figure, a field of 3x3 is used and intersections are done up to level 3.

The test and recursive structure and sequence can be compared to a genealogical Ahnentafel, the unions to marriages, the number 15 to the proband, having two parents, four grandparents, eight great-grandparents, et cetera.

Checking results

While we can run the program and see the results (the program optionally creates an SVG file), we have to have a mechanism to check if the results are correct.

Luckily we are doing geometry, we are doing mathematics, we are doing set theory, so we can use that to check our results.

Checks are done in each step, so during the processing of two polygons. Besides a union (u), an intersection (i) is done. The area is calculated of the original polygons (p and q), of the union, and of the intersection. And it always must be that the area of the union equals to the area of both input polygons, minus the area of the intersection. So: A(u) == A(p) + A(q) - A(i). A simple check, all done by the library itself.

So we can run the check for thousands of times, and for various levels, field sizes, boxes and triangles. It now also runs for counter clockwise polygons and open polygons.

It is not the case that it was without errors the first time... There have been many errors, especially in the self-tangencies, points were two polygons in a multi-polygon touch each other. That all have been solved. So running this test was absolutely valuable.

Seven levels

After seven levels in a field of 10x10 we might get the next results: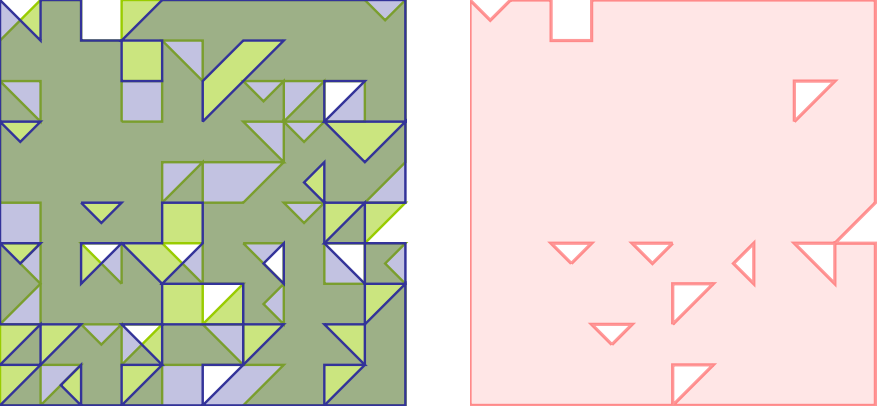



At the left the two input polygons (green and blue), at the right the union in red. After these seven levels in the 10x10 field, the unions are that large that they nearly completely fill up the whole area.

Last month I did most tests in this configuration, 10x10 and up to 7 levels. 7 levels results in 255 tests, this is 2⁸-1

Twelve levels

Twelve levels results in 2¹²-1 unions and shows in a 100x100 field like this:


and we can go further and further, but for Boost.Geometry the tests do not give problems anymore. It all runs fine. This test (so 8191 unions and intersections ending in this complexity) runs in two seconds on my current machine (actually, to be precise, it is doing the union twice because the overlay function is reused in other tests as well).

Unit test

It is a sort of a unit test, because the program checks itself. I also use it as a unit test. But note that the program is based on random input, and that a 30-level test resuls in 2³⁰-1 unions and intersections (~1G). So it runs for a while, and including this in the standard Boost test suite will not be appreciated. So this recursive_polygons can be run manually, and there are parameters to specify the number of levels, et cetera.

By the way, there are many real unit tests within Boost.Geometry, there are currently 118 source files using the (great!) Boost.Test library, and some of them use polygons which are created by this testprogram as their input.

Conclusion

This recursive polygon unit test has been very valuable and, besides that, such tests are nice to program. The whole program, links are given above, is rather short, and it is of course Open Source. This test might be useful for other libraries as well.