Spherical Side Formula

This blog describes an algorithm and a formula to determine the side of one point relative to a segment (two other points), all three points located on a sphere.

The side informarmation is necessary for Boost.Geometry. It is used, among others, in the within algorithm, to check if a point is inside a polygon (point in polygon). With the spherical version of side, it can be checked if a point on a sphere (the earth) is inside a spherical polygon (e.g. a polygon measured in latitude, longitude).

It is also known as orientation (see also here and here)

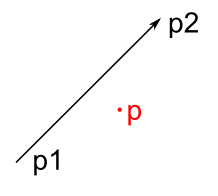
The Cartesian side is shown below. Point p is on the right side of segment p1-p2:


A visualization of ths spherical side is shown below, also here, point p is right of segment p1-p2.


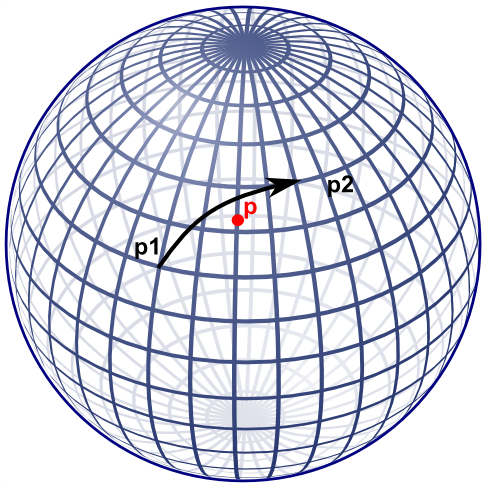
Note that if the cartesian side formula would be used on lat-long coordinates, this specific point would result on the left side.

Former approach

Boost.Geometry's former approach for spherical side used the useful aviation formulae of Williams, listed here. That did work but I was not completely satisfied about it:

• it takes two * (3 cos, 3 sin, 1 atan) for the course, and then another 2 sin, and 1 asin, so in total 17 goniometric functions
• it is non defined at the poles
• I don't understand it fully, it seemed to me that there should be an easier way

An obvious alternative is translate to 3D cartesian coordinates and why not? After working this out a bit, it appeared that it indeed requires less goniometric functions. These goniometric functions are less performant and less precise, so if they can be avoided, the better. Also the new approach is also relatively easy, from mathematical perspective.

New approach

The new approach also uses sin and cos, but  less: for each of the points: 2 sin and 2 cos, in total 12 goniometric functions. Less then the former 17. More important, by design of Boost.Geometry, these might be precalculated such that for a spherical polygon it is not necessary to recalculate this again and again.

Besides that, the algorithm is easier to follow.

The algorithm

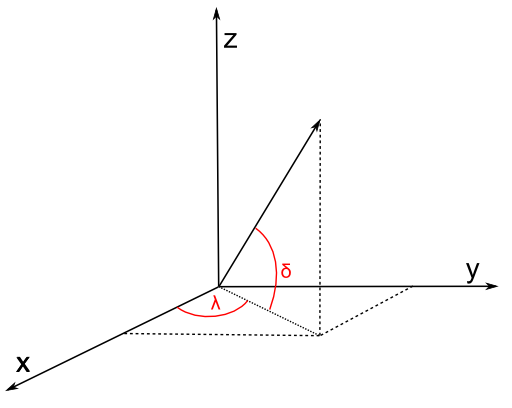
Let us calculate a plane through the two points of the segment, and the center of the sphere. This is the plane also containing the Great Circle. Let us then calculate at which side of the plane the point is located, either left of the plane, or right of the plane, or on the plane itself. The side with respect to the plane is also the side of the point with respect to the segment on the sphere.

To calculate a plane, all three points are transformed from spherical coordinates (longitude, latitude) to cartesian coordinates (x, y, z). Described a.o. here with clear images. We can use the unit sphere, it is not necessary to take the radius of the Earth (or another sphere or sphere-like object) into account. Amsterdam, for example, then lies somewhere here: (0.614161755 0.042946374 0.788010754).


Converting can conveniently be done using Boost.Geometry's transform algorithm (if p1 is stored in cs::spherical_equatorial):

        typedef model::point<coordinate_type, 3, cs::cartesian> point3d;
        point3d c1, c2, c3;
        transform(p1, c1);
        transform(p2, c2);
        transform(p, c3);



Then we define a plane through the center of the Earth (0,0,0) and the two points. We use the generalized plane equation for that (a x + b y + c z + d = 0), described e.g. here. This is done by taking the cross product of the two vectors (a vector is here: a mathematical vector). These two vectors are normally called v and w. Because we use (0,0,0) the points are the vectors, we don't have to subtract anything to create a vector. So v is equivalent to c1, w is equivalent to c2.

The cross product is the normal vector, called n, normal to the plane, so perpendicular to the great circle of the two points. So we can take the cross product:

vector_type const n = geometry::cross_product(v, w);

We now have our generalized plane equation. To make that explicit, we can use the conventional symbols a, b, c:

        coordinate_type const a = get<0>(n);
        coordinate_type const b = get<1>(n);
        coordinate_type const c = get<2>(n);

For the generalized plane equation, we should calculate d by subsituting one of the points going through the plane. Let us take (0,0,0)! By taking 0,0,0, all terms a x, b y, c z will be zero, so d is zero. Therefore we don't have to calculate d.

        double const d = 0;

The generalized plane equation has the property that, if you substitute another point, it is either on the plane (then the result = 0), or at one side of the plane (then the result is positive), or at another side of the plane (then the result is negative). Just like the Cartesian side, described above. And that is exactly what we need:

distance_measure = a * get<0>(c3) + b * get<1>(c3) + c * get<2>(c3) + d;

and we have the result:

int side
            = distance_measure > 0 ? 1 // left
            : distance_measure < 0 ? -1 // right
            : 0;

Spherical Side Formula

We used convenient vector calculation here, making it a mathematical exercise. Of course we could write them all out and get a lot of goniometric functions back.

One big note here: geographers (as I am) always refer to coordinates on a sphere by defining 0 at the equator. But mathematicians define 0 at the upper pole of a sphere. Watch out, it is different. This blog assumes the geographic convention, so assumes a spherical equatorial coordinate system.

Let's present it as mathematic formulae (thanks to mathcast):



The first formula converts to x,y,z. Be sure to enter all angles in radians. Also, be sure that λ is longitude (and comes first in Boost.Geometry) and δ is latitude (there are many conventions for this but I'm using them from here, and not from here and here and here). Latitude is 0 at the equator, 90 at the North Pole (again: mathematicians use 0 at the North Pole, 90 at the aquator; that is known as the spherical (polar) coordinate system, we now refer to the spherical equatorial coordinate system).

The second formula is the cross product and defines the terms of the generalized plane equation. The third formula calculates the distance measure (dm). Because (2) and (3) do not have repetitive clauses, they could be combined into (4) and then, if wished, again, with the conversion, into (5).

The sixth pseudo-formula then defines the result, it is an interpretation of the distance measure dm.

Ellipsoidal Earth

The Earth is not spherical but approximates an ellipsoid, it is flattened at the poles. But the described spherical side formula works well on Earth. Let me try to prove that (note: I'm a geographer, not a mathematician).

A location defined by (λ, δ) essentially means a vector, either on a sphere, or on an ellipsoid. These vectors always have the same direction, so the same on a sphere as on an ellipsoid. Their lengths differ (on an ellipsoid they are often shorter) but the length of a vector does not influence the plane it encompasses. Therefore the plane formed by two locations and the center of the Earth is exactly the same plane as it is using a perfect sphere.

So: two points (a segment), on a sphere or on an ellipsoid, define the same plane.

The same applies for the third point. It is also a vector, having a direction. That vector, either on a sphere or on an ellipsoid, is located at the same side of the plane.

Q.E.D.

Code

Because of the formulae above, I don't give (pseudo)code. It is quite easy. I created a small Excel sheet containing the formula is here. It contains this example (on this useful site): gcmap The formula is also in Boost.Geometry.

Summary

Using some high-school mathematics I presented an algorithm and a formula to calculate at which side a point is with resepect to a segment, on a sphere or on the Earth. Google did not find this for me. So I hope that it will be of some use for some people. At least, it is useful for Boost.Geometry